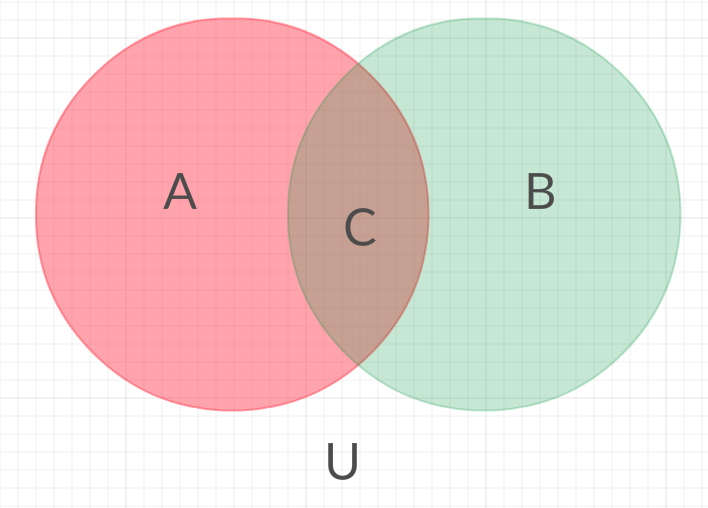
$$ P(A|B) = \frac{C}{B} = \frac{C}{B} \cdot \frac{B}{U} / \frac{B}{U} = \frac{C}{A} \cdot \frac{A}{U} / \frac{B}{U} = P(B|A) \cdot \frac{A}{U} / \frac{B}{U} = P(B|A) \cdot P(A) / P(B) $$
$$ => P(A|B) \cdot P(B) = P(B|A) \cdot P(A) $$
即
$$ \frac{C}{B} \cdot \frac{B}{U} = \frac{C}{A} \cdot \frac{A}{U} = \frac{C}{U} $$