Web中的加密算法

发布于 2018-01-02 17:26:57

Content

通信加密对人类来说是刚性需求。

  • 术语
    • 对称密钥加密
    • 非对称密钥加密（公私钥）
    • 数字签名
  • 作用
    • 信息保密
    • 身份确认
    • 不可抵赖
    • 数据完整
  • 历史
    • 经典密码学：通过文本频率分析破解了
    • 中世纪到第二次世界大战：密码大战
    • 现代密码学：与计算机的结合
  • 常见算法
    • 对称性加密
      • DES算法、3DES算法、IDEA算法、AES算法
      • 缺点：密钥的分发和管理非常复杂
    • 非对称性加密
      • RSA算法、ElGamal算法、椭圆曲线加密算法
      • 缺点：实现速度慢，不适合通信负荷较重的情况
    • 混合加密
      • 选用一个随机数作为会话的对称密钥，通过非对称加密发送给对方，以后的通信都通过这个随机密钥来进行
    • 散列函数
      • 产生定长的消息摘要
      • 常见的散列算法：MD2、MD4、MD5、SHA、SHA-1
  • 应用
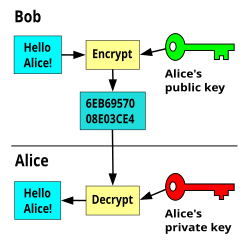
    • 数字签名
      • 作用
        • 确认是由签名者发出
        • 发送者不可抵赖
        • 确认内容完整性
      • 实现
        • 消息摘要 + 非对称加密
      • 过程
        • 发送方：消息 --散列函数--> 消息摘要 --私钥--> 数字签名 => 消息+数字签名
        • 接收方：数字签名 --公钥--> 消息摘要 --> 验证是否相等
      • 数字信封
        • 两组非对称密钥对
        • 一个对称私钥
        • 对通信过程的私密性做了保障
        • 发送
          • 发送方的私钥用于数字签名
          • 接收方的公钥用于加密对称私钥，生成数字信封
          • 对称私钥用于消息原文、数字签名，得到密文
        • 接收
          • 接收方私钥解开数字信封，得到对称私钥
          • 用对称私钥解开密文，得到消息原文、数字签名
          • 验证数字签名
    • 数字证书
      • 种类
        • 服务器证书
        • 电子邮件证书
        • 客户端证书
      • 应用
        • HTTPS
          • 证书中心（certificate authority，CA）用自己的私钥为大家的公钥做认证，生成数字证书
          • 发送方在数字签名的同时，附上数字证书
          • 接收方用CA的公钥解开数字证书，得到发送方的公钥，然后用它来验证数字签名
    • HMAC

      • Keyed-hash message authentication code 密钥散列消息认证码

      • 组成

        • 散列函数
        • 加密密钥

      • 作用

        • 保证数据完整性
        • 用作某消息的身份验证

      • 过程

        • 公式：
        H为密码散列函数（如MD5或SHA-1）
K为密钥（secret key）
m是要认证的消息
K'是从原始密钥K导出的另一个秘密密钥（如果K短于散列函数的输入块大小，则在右边填充（Padding）零；如果比该块大小更长，则对K进行散列）
|| 代表串接
⊕ 代表异或（XOR）
opad 是外部填充（0x5c5c5c…5c5c，一段十六进制常量）
ipad 是内部填充（0x363636…3636，一段十六进制常量）

      • 应用

        • Web身份验证
          • 过程
            1. 客户端发出登录请求（假设是浏览器的GET请求）
            2. 服务器返回一个随机值，并在会话中记录这个随机值
            3. 客户端将该随机值作为密钥，用户密码进行hmac运算，然后提交给服务器
            4. 服务器读取用户数据库中的用户密码和步骤2中发送的随机值做与客户端一样的hmac运算，然后与用户发送的结果比较，如果结果一致则验证用户合法
          • 在这个过程中，可能遭到安全攻击的是服务器发送的随机值和用户发送的hmac结果，而对于截获了这两个值的黑客而言这两个值是没有意义的，绝无获取用户密码的可能性，随机值的引入使hmac只在当前会话中有效

      • Python实现

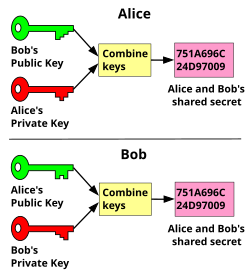
    • ECDH密钥交换
      • DH和ECDH原理
        • 质数p、底数g、Alice公私钥A、a，Bob公私钥B、b
        • Q = (g^a mod p) ^ b mod p
          • a、b 可互换(?)
      • ECC算法和DH结合使用，用于密钥磋商，这个密钥交换算法称为ECDH。交换双方可以在不共享任何秘密的情况下协商出一个密钥。ECC是建立在基于椭圆曲线的离散对数问题上的密码体制，给定椭圆曲线上的一个点P，一个整数k，求解Q=kP很容易；给定一个点P、Q，知道Q=kP，求整数k确是一个难题。ECDH即建立在此数学难题之上。
      • 密钥磋商过程：
        • 假设密钥交换双方为Alice、Bob，其有共享曲线参数（椭圆曲线E、阶N、基点G）。
          1. Alice生成随机整数a，计算A=a*G。 #生成Alice公钥
          1. Bob生成随机整数b，计算B=b*G。 #生产Bob公钥
          1. Alice将A传递给Bob。A的传递可以公开，即攻击者可以获取A。
        • 由于椭圆曲线的离散对数问题是难题，所以攻击者不可以通过A、G计算出a。
          1. Bob将B传递给Alice。同理，B的传递可以公开。
          1. Bob收到Alice传递的A，计算Q =b*A #Bob通过自己的私钥和Alice的公钥得到对称密钥Q
          1. Alice收到Bob传递的B，计算Q`=a*B #Alice通过自己的私钥和Bob的公钥得到对称密钥Q’
        • Alice、Bob双方即得Q=b*A=b*(a*G)=(b*a)*G=(a*b)*G=a*(b*G)=a*B=Q' (交换律和结合律)，即双方得到一致的密钥Q。

图解

数字签名

Diffie–Hellman key Exchange

References

comments powered by Disqus